'll Hacker

EVI$ION 겨울방학 코테스터디 1주차 과제 본문

Dev

EVI$ION 겨울방학 코테스터디 1주차 과제

씨이오가 되자 2025. 1. 3. 14:11
Contents
728x90

그리디 알고리즘 

눈앞의 이익만 우선 추구하는 알고리즘

최적해를 찾을 수 있으면 그것을 목표로 삼고 찾기 어려운 경우에는 주어진 시간 내에 그런대로 괜찮은 해를 찾는 것을 목표로 삼는다 - 그래서 대부분 최적화 문제를 대상으로 함

 

예를 들어, n개의 정점을 가지고 사이클을 이루지 않은 총 n-1개의 간선으로 이뤄지는 최소 신장 트리를 만들고자 한다.

아직 간선이 하나도 없는 상태라고 하면, n-1개의 간선이 될 때까지 집합을 키워나가게 된다. 

이때, 어떤 간선을 선택할지 결정해야한다.

최소신장트리같은 경우에는 간선을 하나 더할 때마다 해당 간선이 기존에 선택된 간선들과 사이클이 형성되면 안된다.

Greedy(c)
{
	s <- 공집합;
    while (c는 공집합이 아니고 S는 아직 온전한 해가 아님){
    	x <- c에서 원소 하나 선택; 1)
        집합 c에서 x를 제거;
        if(s에 x를 더해도 됨) then s<-s∪{x}; 2)
    }
    if(s가 온전한 해임) then return s;
    else return "해없음!";
}

1) 원소를 선택하는 기준이 눈앞의 이익을 우선

2) 원소를 하나 더하기 전에 해당 원소를 더함으로써 온전한 해가 될 가능성이 없어지지 않았는지 체크 

 

최적해 보장되지 않는 예)

1. 이진트리의 최적합 경로 찾기

각 노드가 양의 가중치를 갖고 있는 이진트리가 있다. 루트부터 시작해서 왼쪽으로 분기할지 오른쪽으로 분기할지를 매단계마다 결정해야하는데, 트리의 내용은 사전에 알지 못해서 임의의 노드에 이르면 그제서야 그 노드의 자식에 할당된 가중치가 공개된다. 그리고 리프노드를 만나면 끝나는 알고리즘이다. 

이 과정에서 만난 노드에 있는 가중치 합이 이 경로의 점수이므로 이 합을 최대화하는 알고리즘을 찾아야 하는게 관건이다.

가보지 않은 어떤 노드가 다른 모든 경로의 합보다 큰 가중치를 갖고 있을 가능성이 있기 때문에

모든 노드를 보기 전에는 최적해 보장되지 않는다.

 

2. 보따리 문제

부피가 M인 보따리와 이 보따리에 넣으려 하는 n개의 물건이 있다.

물건 i의 부피는 wi이고, 이것을 보따리에 넣을 경우 Pi의 가치가 있다.

물건들의 전체 부피 합이 M을 넘지 않도록 하면서 가치가 최대가 되도록 보따리에 물건들을 넣는다.

보따리 용량을 초과하지 않은 한 단위 부피당 가치가 가장 큰 물건순 서로 각 물건을 보따리에 추가된다.

근데 이런 방식의 그리디 알고리즘은 최적해를 보장하지 못한다.

이 문제를 0-1 Knapsack Problem이라고 부른다.

보따리 문제에서 물건을 가를 수 있다면 최적해 보장된다. 즉, 단위 부피당 가치가 가장 큰 물건 순서로 각 물건을 보따리에 추가하다가 어떤 물건을 넣으려는 순간 보따리 용량을 초과하면 남은 용량에 들어갈 만큼만 잘라넣으면 된다.

이 문제를 Fractional Knapsack Problem이라고 부른다. 

 

3. 동전 바꾸기 

500, 100, 50, 10, 5, 1이 있고 3256원을 만들고자 할 때 가장 적은 개수의 동전을 사용한다면?

500 x 6 = 3000, 100 x 2 = 200, 50 x 1 = 50, 5 x 1 = 5, 1 x 6 = 6 으로 총 11개의 동전을 사용

 

500, 400, 100, 75, 50이 있고 1300원을 만들고자 할 때 가장 적은 개수의 동전을 사용한다면?

500 x 2 = 1000, 100 x 3 = 300으로 총 5개의 동전을 사용

최적해를 구하자면, 500 x 1 = 500, 400 x 2 = 800으로 총 3개의 동전을 사용

이 문제는 동적 프로그래밍으로 최적해를 구할 수 있다. 

 

최적해 보장되는 예)

1. 최소 신장 트리 ex) 프림 알고리즘, 크루스칼 알고리즘

ex) 프림 알고리즘

입력: 그래프 G = (V, E) (V는 정점 집합, E는 간선 집합)
출력: 최소 신장 트리 T

1. 모든 정점 v ∈ V에 대해 key[v] ← ∞
2. 임의의 시작 정점 s ∈ V를 선택하고, key[s] ← 0
3. 모든 정점 v ∈ V에 대해 parent[v] ← NIL
4. 우선순위 큐 Q에 모든 정점 v ∈ V를 추가 (key를 기준으로 정렬)

5. while Q가 비어 있지 않으면:
    5.1 u ← Q에서 key[u]가 가장 작은 정점 제거
    5.2 u를 최소 신장 트리에 추가
    5.3 for u에 인접한 모든 정점 v ∈ Adj[u]:
        5.3.1 if v ∈ Q and 가중치(u, v) < key[v]:
            5.3.1.1 parent[v] ← u
            5.3.1.2 key[v] ← 가중치(u, v)
            5.3.1.3 Q에서 key[v] 갱신

6. 최소 신장 트리 T를 parent 배열로 반환

 

프림 알고리즘이란?

최소 신장 트리 구현에 사용되는 알고리즘, 시작 정점에서 정점을 추가해가며 단계적으로 트리를 확장하는 기법

 

매 순간 최선의 조건을 선택하는 그리디 알고리즘을 기반함.

즉, 탐색 정점에 대해 연결된 인접 정점들 중 비용이 가장 적은 간선으로 연결된 정점을 선택함

  • 시작 단계는 시작 노드만이 MST 집합에 속함
  • 트리 집합에 속한 정점들과 인접한 정점들 중 가장 낮은 가중치의 간선과 연결된 정점에 대해 간선과 정점을 MST 트리 집합에 넣음. (사이클을 막기 위해 연결된 정점이 이미 트리가 속한다면 그 다음 순서를 넣음)
  • 2번 과정을 MST 집합의 원소 개수가 그래프의 정점의 개수가 될 때까지 반복함
    (간선의 가중치를 더해서 최소 신장 트리 비용 산출)

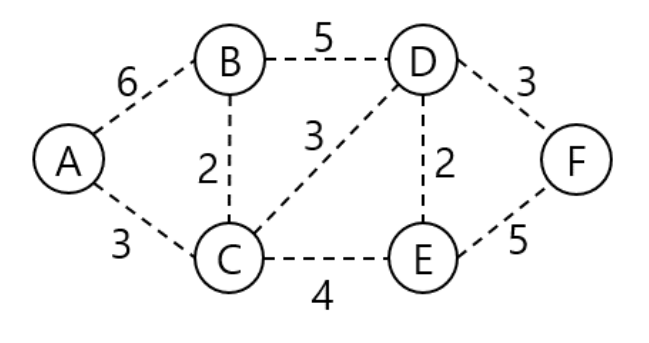
[진행 전]

우선순위큐 : N = 정점 번호, W = 비용.

정점 번호 [1] [2] [3] [4] [5] [6]
해당 정점 A B C D E F
visited F F F F F F

 

[진행 중]

step 1. 우선 시작 정점을 하나를 A라고 정한다. 우선순위 큐에 A를 넣는다. 처음에는 시작 정점의 간선 비용은 0으로 설정

우선순위 큐에서 비용이 가장 작은 정점 하나를 꺼냄. 여기서는 시작정점 A 밖에 없어서 A가 꺼내짐 (N = 1, W = 0)

step 2. A 정점을 방문처리. visited[1] = True

정점 번호 [1] [2] [3] [4] [5] [6]
해당 정점 A B C D E F
visited T F F F F F

 

step 3. 간선 비용의 총 합을 구하는 변수 sum에 정점 A의 비용 = 0을 더한다. sum = 0

step 4. A 정점이랑 연결된 B와 C를 우선순위 큐에 넣는다. (N = 2, W=6 / N = 3, W = 3)

step 5. 우선순위 큐에서 가장 작은 정점 하나를 꺼냄 

step 6. C 정점을 방문처리. visited[3] = True

정점 번호 [1] [2] [3] [4] [5] [6]
해당 정점 A B C D E F
visited T F T F F F

step 7. 간선 비용의 총 합을 구하는 변수 sum에 정점 C의 비용 = 3을 더한다. sum = 3

...

이렇게 반복하면 모두 방문된 상태가 되고, 

정점 번호 [1] [2] [3] [4] [5] [6]
해당 정점 A B C D E F
visited T T T T T T

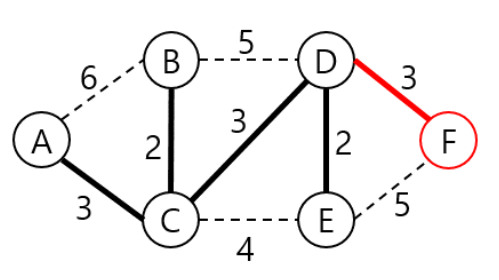
이렇게 최소 신장 트리가 나오게 된다.

sum = 13으로 최소 신장 트리 구축의 비용은 13이다.

 

2. 회의실 배정 문제

회사에 회의실이 1개 있는데, 사용하기 위해서는 원하는 회의 시작시간과 종료시간을 예약해야한다.

겹치는 회의가 없게 하면서 가장 많은 수의 회의를 소화가능하게 하는게 목표이다.

(11시에 회의가 끝나고 바로 11시에 시작하는 것도 가능하다.)

입력: n개의 회의 (회의 i는 시작 시간 start[i]와 종료 시간 end[i]를 가짐)
출력: 선택된 회의들의 집합

1. 각 회의를 종료 시간 기준으로 오름차순 정렬한다.
    - 정렬 기준: end[i] 오름차순
2. 선택된 회의 집합 selected를 초기화한다.
3. 마지막으로 선택된 회의의 종료 시간을 기록할 변수 last_end ← 0
4. for i = 1 to n:
    4.1 if start[i] ≥ last_end:
        4.1.1 회의 i를 selected에 추가
        4.1.2 last_end ← end[i]
5. selected를 반환

종료 시간이 빠른 순서대로 회의를 정렬하여 가장 많은 회의를 선택하기 위해 필요한 그리디 선택이다. 새로 선택한 회의의 시작 시간이 이전에 선택된 회의의 종료 시간 이후인지 확인한다. 조건을 만족하면 해당 회의를 선택하고, last_end값을 업데이트한다. 

예를 들어, 8개의 회의가 신청된 상황에서 종료시간이 빠른 순서로 정렬한 결과가 다음과 같다.

(3, 5), (1, 6), (6, 7), (5, 9), (8, 13), (7, 14), (12, 18), (16,20)

먼저 1번 회의 (3, 5)은 무조건 들어간다. 1번 회의가 끝나는 시간은 5이다. 그다음 (1, 6)은 앞에 배정된 회의와 겹치는 시간이 있으므로 제외한다. 또 다음 (6, 7)은 겹치지 않아 포함된다. 2번 회의가 끝나는 시간은 7이다. (5, 9)는 제외된다. (8, 13)은 포함된다. 끝나는 시간은 13이다. (7, 14), (12, 18)은 제외된다. (16, 20)이 포함된다.

즉, 차례가 왔을 때 자신의 시작 시간이 이미 배정된 회의 중 맨 마지막에 끝나는 것보다 뒤면 포함시킨다.

따라서, (3, 5), (6, 7), (8, 13), (16, 20) 이 된다.

 

3. 그 밖의 예

다익스트라 알고리즘

허프만 코딩 알고리즘 

 

5585, 거스름돈, C++ 

 

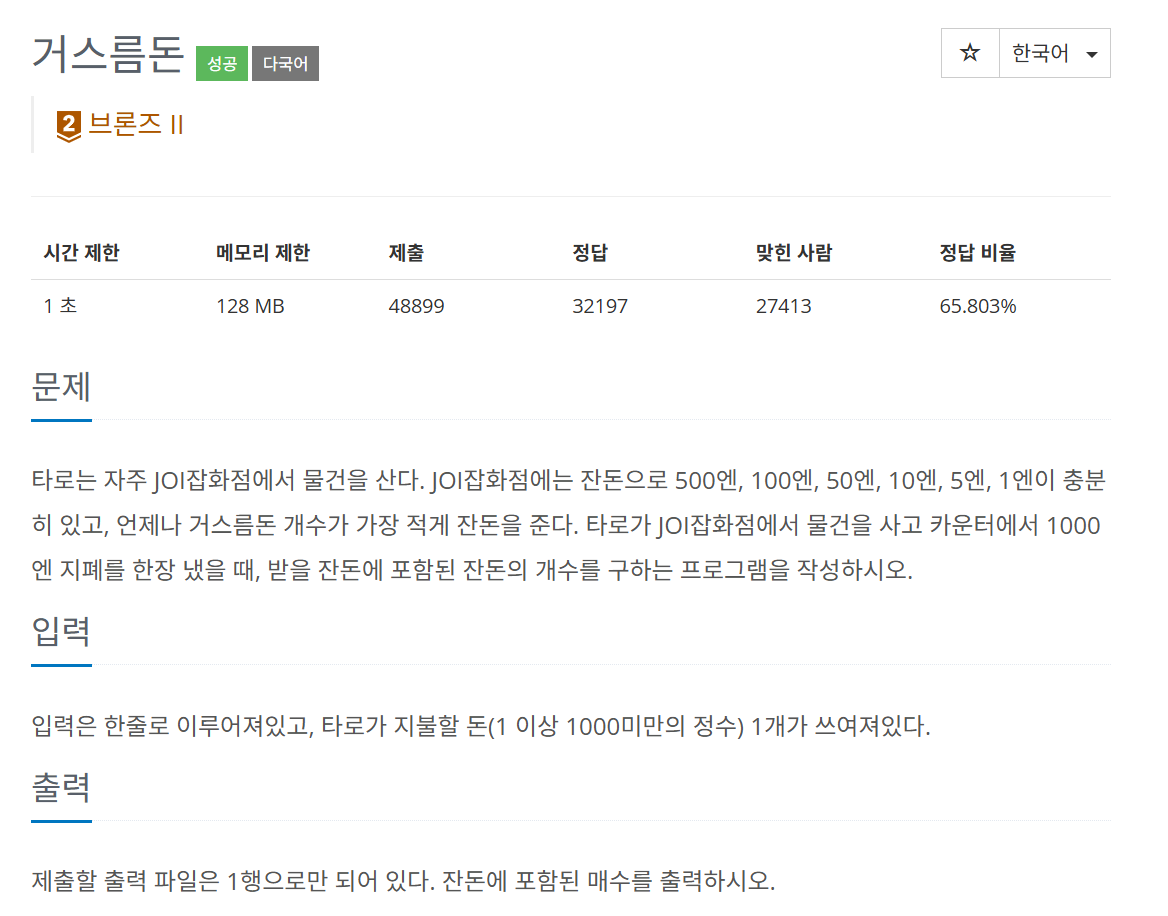
거스름돈 개수가 가장 적게 잔돈을 주는 알고리즘을 짜야되는데 최적해가 보장되지는 않지만 그리디 알고리즘을 사용하면 구현이 가능하다. 앞에서 언급한 동전의 개수 구하기와 다르게 이것은 입력값의 동전 개수가 아니고 1000엔에서 380을 거슬러줄 때 잔돈의 개수를 구하는 것으로 이해하였다. 

테스트 케이스

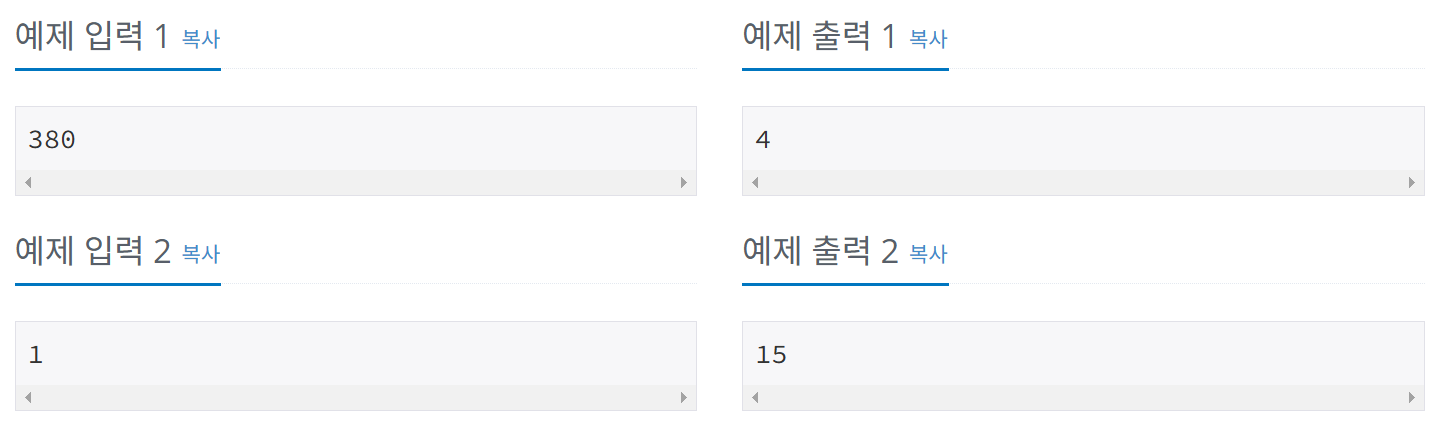
380을 입력하면, 1000-380=620에서 개수를 구하면 된다.

620 = 500 x 1 + 120

120 = 100 x 1 + 20

20 = 10 x 2 + 0

나머지가 0일 될 때까지 반복문 돌리면 될 것 같다.

1을 입력할 때도 마찮가지다.

다음은 내가 구현한 C++ 코드이다.

#include <iostream>
#include <stack>
#include <algorithm>
using namespace std;

int counter = 1000; // 물건을 사고 카운터에서 1000엔 지폐를 한장 낸 경우 , 전역변수로 두기
int arr[6] = { 500, 100, 50, 10, 5, 1 };

void solution(int paper)
{
	int remain = counter - paper; 
	int sum = 0;
	
	for (int i = 0; i < 6; i++)
	{
		sum += remain / arr[i];
		remain %= arr[i];

	}
	// 출력
	cout << sum;
}

int main()
{
	int paper = 0;
	// 입력
	cin >> paper;

	// 연산
	solution(paper);

	return 0;
}

 

 

11399, ATM, C++

풀이는 다음 링크를 통해서 보실 수 있습니다.

https://successing.tistory.com/87

 

 

BOJ - 11399 ATM 문제 풀이

https://www.acmicpc.net/problem/11399   문제를 이해를 해보자면 모두 5명이고각 사람 당 돈을 인출하는데 필요한 시간을 5번 입력받게되는데, 문제 그대로 이해하면 될 것 같다.각 사람 당 기다리는 시

successing.tistory.com

1213, 팰린드롬 만들기, C++

팰린드롬은 좌우 대칭 구조를 가져야 해서 문자열의 각 문자는 짝수 개이어야 하고, 

문자열의 길이가 홀수인 경우, 가운데에 올 수 있는 문자는 최대 하나만 홀수개이어야한다.

각 문자의 개수를 세고, 짝수 개와 홀수 개를 판별한 후,

홀수 개의 문자가 2개 이상이면 팰린드롬을 만들 수 없어서 "I'm Sorry Hansoo"를 출력

그렇지 않은 경우 팰린드롬 구성가능

문자의 절반을 앞쪽에 배치하고, 홀수 개의 문자가 있다면, 이를 가운데에 추가한다.

앞쪽에 배치한 문자열을 뒤집어 붙여 팰린드롬을 구현한다.

#include <iostream>
#include <string>
using namespace std;
string ChangeString(string original, int* count,int flag)
{
	string c; int j = 0; int value, mod, cnt = 0, iter = 0; char temp;
	for (int i = 0; i < 26; i++) {//앞에서
		value = count[i] / 2;
		if (count[i] > 0) {
			for (int j = 0; j < value; j++) {
				c += i + 'A';    //현재 문자열 저장
			}
		}
	}
	for (int i = 0; i < 26; i++) { //가운데
		if (count[i] % 2 ==1)
		{
			c += i + 'A';
		}
	}
	for (int i = 25; 0 <= i; i--) //뒤로
	{
		value = count[i] / 2;
		for (int j = 0; j < value; j++) {
			c += i + 'A';    //현재 문자열 저장
		}
	}
	return c;
}
string CountString(string original)
{
	int count[26] = { 0, },flag=0; //아스키 코드 A ~ Z 25개 여분으로 26개 배열선언
	string result;

	for (int i = 0; i < original.size(); i++)
	{
		count[original[i] - 'A']++;  //글자별로 개수세기
	}
	for (int i = 0; i < 26; i++)
	{
		if (count[i] % 2 != 0)
		{
			flag++;
		}
	}
	if (flag < 2)
		result = ChangeString(original,count,flag);
	else
		result = "I'm Sorry Hansoo";
	return result;
}

int main()
{
	//입력
	string original,result;
	cin >> original;

	//연산
	result = CountString(original);


	//출력
	cout << result;
	
}

 

 

참고)

한빛미디어, 쉽게 배우는 알고리즘, 문병로 지음 

https://8iggy.tistory.com/159

 

 

728x90
저작자표시 비영리 변경금지

'Dev' 카테고리의 다른 글

EVI$ION 겨울방학 코테스터디 3주차 과제  (0) 2025.01.18
EVI$ION 겨울방학 코테스터디 2주차 과제  (0) 2025.01.11
BOJ 1543 문서검색 문제  (2) 2024.09.27
BOJ - 11399 ATM 문제 풀이  (0) 2024.09.26
GitHub 사용법  (0) 2024.09.20
'Dev' Related Articles more